Представление рациональных чисел

— Чему равна лошадиная сила?
— Это сила лошади весом один килограмм и ростом один метр
—Да где же вы видели такую лошадь?
— А ее вообще мало кто видел. Она хранится под аргоновый колпаком в Палате мер и весов под Парижем.

Представить произвольное вещественное число при помощи конечного числа элементов, способных принимать лишь ограниченный набор значений (а именно таковы все цифровые представления данных), разумеется, невозможно. Максимум, что можно сделать — это найти то или иное рациональное приближение для такого числа, и оперировать им.

Примечание
На самом деле, возможно точное, а не приближенное представление вещественных

чисел рациональными — не одиночной дробью, а сходящейся бесконечной последовательностью дробей, так называемое Гильбертово сечение. Конечным представлением служит не сама последовательность, а правило ее формирования. Из-за своей сложности такое представление крайне редко используется в вычислительных системах и никогда не реализуется аппаратно.

Два основных представления рациональных чисел, используемых в компьютерах, — это представления с фиксированной и плавающей точкой. Интерпретирующие системы (например, MathCAD) иногда реализуют и собственно рациональные числа, представляемые в виде целых числителя и знаменателя, но процессоры, умеющие работать с такими числами на уровне системы команд, автору неизвестны.
Представление с фиксированной точкой (рис. 1.3) концептуально самое простое: мы берем обычное двоичное число и объявляем, что определенное количество его младших разрядов представляет собой дробную часть в позиционной записи. Сложение и вычитание таких .чисел может выполняться при помощи обычных целочисленных команд, а вот после умножения и перед делением нам надо, так или иначе, передвинуть двоичную запятую на место.

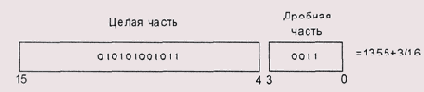
Рис. 1.3. Число с двоичной фиксированной точкой

Примечание
В русском языке принято называть разделитель целой и дробной частей позиционной дроби запятой, а в английском — точкой. Современная вычислительная терминология формировалась на английском языке, и английские словосочетания fixed-point и floating-point часто переводились на русский язык буквально, поэтому словосочетания "фиксированная точка" и "плавающая точка" прочно вошли в русскую компьютерную лексику, и мы будем использовать именно их.

Современные процессоры обычно не предоставляют арифметических операций с фиксированной точкой, однако никто не запрещает программисту или разработчику компилятора реализовать такие операции на основе стандартных целочисленных операций и команд битового сдвига.
Если нам необходима точность вычислений, определенная количеством десятичных знаков (например, при подсчете рублей с точностью до копеек), нужно помнить, что большинство десятичных дробей в позиционной двоичной записи представляют собой периодические (с бесконечным числом знаков) дроби. Для обеспечения требуемой точности нам следует либо иметь дополнительные двоичные позиции, либо вместо фиксированной двоичной использовать фиксированную десятичную точку: складывать такие числа по-прежнему можно с помощью целочисленных операций, но коррекцию умножения и деления необходимо выполнять с помощью умножения (деления) на степень десяти, а не на степень двойки.
В научных и инженерных вычислениях и цифровой обработке сигналов шире применяются числа с плавающей двоичной точкой. Дело в том, что исходные данные для таких вычислений обычно являются результатами измерений физических величин. Все физически реализуемые способы измерений сопровождаются ошибками: для объяснения этого печального факта часто ссылаются на принцип неопределенности Гейзенберга [Карнап 1971], но при практических измерениях гораздо большую роль играют следующие виды ошибок.

1. Тепловые шумы — температурные колебания измеряемого объекта и измерительного инструмента.
2. Инструментальные погрешности, обусловленные различными ошибками при изготовлении или калибровке инструмента или изменением его параметров с момента последней калибровки, например, за счет механического износа.
3. Методологические ошибки, обусловленные не только неумением пользоваться
инструментом, но и тем фактом, что наши инструменты не имеют непосредственного контакта с явлением, которое мы хотим измерить: например, измеряя динамику валового внутреннего продукта, мы, в действительности, измеряем также и эффекты, обусловленные динамикой денежной массы. Возможна и обратная ситуация, когда наш инструмент имеет слишком тесный контакт с измеряемым объектом и искажает его поведение. Из школьного курса физики известны такие источники методологических ошибок, как падение напряжения на вольтметре или внутреннее сопротивление амперметра.

Если с принципом Гейзенберга бороться невозможно, то тепловые и инструментальные ошибки можно уменьшать, первые — снижением температу-Pbi, а вторые — большей тщательностью изготовления и калибровки, ужесточением условий эксплуатации и хранения или совершенствованием самого инструмента (например, интерферометрический лазерный дальномер при равной тщательности изготовления будет намного точнее рулетки).
Однако ни абсолютный нуль температуры, ни абсолютная точность изготовления физически недостижимы, и даже приближение к ним в большинстве ситуаций недопустимо дорого.
Сомневающемуся в этом утверждении читателю предлагается представить, во что бы превратилась его жизнь, если бы при взвешивании продуктов в магазине сами продукты и весы охлаждались хотя бы до температуры жидкого азота, а плотницкий метр надо было бы хранить с теми же предосторожностями, что и метрологический эталон.
Поэтому на практике целесообразно смириться с погрешностями измерений, а на приборе указать точность, которую его изготовитель реально может гарантировать при соблюдении пользователем условий хранения и эксплуатации. Полному искоренению подлежат только методологические ошибки, да и с ними во многих ситуациях приходится смириться из-за неприемлемо высокой стоимости прямых измерений.
Относительно дешевый способ повышения точности — многократные измерения и усреднение результата, но этот метод повышает стоимость измерений и, если измерения производятся одним и тем же инструментом, не позволяет устранить инструментальные и методологические ошибки.
И тепловые шумы, и инструменты порождают ошибки, которые при прочих равных условиях пропорциональны измеряемой величине. Десяти метровая рулетка имеет инструментальную ошибку, измеряемую миллиметрами, а десятисантиметровый штангенциркуль — микронами. Поэтому ошибку измерений часто указывают не в абсолютных единицах, а в процентах.
При записи результатов измерений хорошим тоном считается указывать точность этих измерений и не выписывать десятичные цифры (или знаки после запятой), значения которых лежат внутри границ ошибки. Цифры перед десятичной запятой в этом случае заменяются нулями, а после нее -просто отбрасываются. Для сокращения записи больших значений, измеренных с относительно небольшой точностью, в научной и инженерной литературе используется экспоненциальная запись чисел: незначащие (в данном случае — лежащие внутри границ ошибки) младшие десятичные цифры отбрасываются, и после числа добавляется 10^N, где N — количество отброшенных цифр. Обычно рекомендуют нормализовать такую запись, перемещая десятичную запятую на место после старшей цифры (смещение запятой на одну позицию влево соответствует увеличению показателя степени множителя на единицу). В соответствии с этими правилами величина 2128506 ± 20 преобразуется к виду 2,12850х10⁶ (обратите внимание, что младший ноль в данном случае является значащим).
При бытовых измерениях обычно обходятся двумя-тремя значащими десятичными цифрами. В научных и инженерных измерениях используются и большие точности, но на практике измерения с точностью выше шестого десятичного знака встречаются разве что при разработке и калибровке метрологических эталонов. Для сравнения, цифровая телефония обходится 8-ю битами, а аналого-цифровой преобразователь бытовой звуковой карты имеет 12, реже 14 значащих двоичных разрядов. Большинство современных карт считаются 16-битными, но на практике младшие разряды их АЦП оцифровывают только тепловой шум усилителя и собственных старших разрядов, а также ошибки калибровки того и другого. Честные (т. е. такие, у которых все разряды значащие) 16-разрядные АЦП используются в профессиональной звукозаписывающей и измерительной аппаратуре, 24-разрядные АЦП относятся к прецизионной аппаратуре, а 32-разрядные на практике не применяют.
Вычислительные системы широко используют представления чисел с плавающей точкой, только не десятичной, а двоичной (рис. 1.4). Идея этого представления состоит в том, чтобы нормализовать позиционную двоичную дробь, избавившись от незначащих старших нулевых битов и освободив место для [возможно] значащих младших разрядов. Сдвиг, который нужен для нормализации, записывается в битовое поле, называемое порядком. Само же число называется мантиссой.

Рис. 1.4. Число с плавающей двоичной точкой

Число с плавающей точкой, таким образом, состоит из двух битовых полей — мантиссы М и порядка Е. Число, представленное двумя такими полями, равно Мх2^Е. Нормализация состоит в отбрасывании всех старших нулей, поэтому старший бит нормализованной двоичной мантиссы всегда равен 1. Большинство современных реализаций чисел с плавающей точкой используют этот факт для того, чтобы объявить незначащими не только старшие нули, но и эту единицу, и, таким образом, выигрывают дополнительный бит точности мантиссы.
Сложение двух чисел с плавающей точкой состоит в денормализации мантисс (совмещении двоичных точек), их сложении и нормализации результата. Перемножение таких чисел, соответственно, выполняется перемножением мантисс, сложением порядков и опять-таки нормализацией результата.
В некоторых старых архитектурах, например БЭСМ-6, все арифметические операции выполнялись над числами с плавающей точкой, однако существовала возможность выключить нормализацию мантиссы. Ненормализованные числа с плавающей точкой использовались для представления значений с фиксированной точкой, в том числе и целочисленных.
Стандарт языка ANSI С требует наличия 32-битового (8-разрядный порядок и 24-разрядная мантисса) и 64-битового (16-разрядный порядок и 48-разрядная мантисса) представлений чисел с плавающей точкой, которые называются, соответственно, числами одинарной и двойной точности (float и double float или просто double). Числа двойной точности, конечно же, не могут быть результатом прямых измерений физических величин, но позволяют избежать накопления ошибок округления при вычислениях.
Большинство современных процессоров общего назначения и ориентированных на приложения цифровой обработки сигналов (ЦОС) предоставляет операции над такими числами, а зачастую и над числами большей разрядности. Операции практически всегда включают сложение, вычитание, умножение и деление. Часто на уровне системы команд реализуются и элементарные функции: экспонента, логарифм, квадратный корень, синус, косинус и т. д. Процессоры ЦОС нередко предоставляют и отдельные шаги дискретного преобразования Фурье.
Количество операций с плавающей точкой в секунду (Floating Operations Per Second, FLOPS, в наше время чаше говорят о Mflops — миллионах операций в секунду), которые может исполнять процессор, является одной из важных его характеристик, хотя и не для всех приложений эта характеристика критична.

Содержание раздела